GRI Mechanism Reduction
Published:
Understanding Reaction Mechanisms:
In chemistry, a reaction mechanism is the step by step sequence of elementary reactions by which overall chemical change occurs. It is a theoretical compilation that explains in detail what happens at every stage of a chemical reaction. This mechanism is chosen because it is thermodynamically feasible, and has experimental support in isolated species (Intermediate) or other quantitative and qualitative characteristics of the reaction.
In the current project, we are using GRI 3.0 reaction mechanism which is an optimized mechanism designed to model natural gas combustion, including NO formation and reburn chemistry.
Mechanism Reduction:
Mechanism Reduction is a process where we remove redundant reactions from the mechanism with respect to our problem parameters. This helps us to customize or tune the mechanism to our specific requirements so that we have the accurate results pertaining to the problem we are solving. For example, we can reduce a mechanism depending on the specific range of operating conditions we want for the fuel.
Based on the study of hydrocarbons combustion using detailed reaction mechanisms, is an important research area of combustion chemistry. The detailed mechanisms consist of hundreds of chemical species and thousands of reaction steps.
The size of the detailed combustion kinetics mechanisms for surrogates of real fuels makes impossible massive design studies with CFD tools.
Types of Mechanisms and their Applications:
- Detailed:
- Hundreds of species, thousands of reactions for typical Hydrocarbon fuels
- Supposed to work in a wide range of conditions
- But further work is to be implemented with tests
- Skeletal:
- Tens of species, Thousands of reactions for typical Hydrocarbon fuels
- Derived from detailed mechanism by removing redundant species and reactions
- Derived for narrow range of conditions, sometimes for specific problems
- Should be tested at desired range of conditions
- Reduced:
- Tens of species and reactions for typical Hydrocarbon fuels
- Derived from Detailed/Skeletal mechanisms by application of Quasi Steady State or Quasi Equilibrium approximations
- Derived for narrow range of conditions, sometimes for specific problem
- Should be tested at desired range of conditions
- Global:
- Can not be directly derived from previous mechanisms, just a simple model
- Can be applied for restricted range of conditions, only for one type of problem
- Must be tested every time before applications
General Strategy for Mechanism Reduction:
The problem and targets for the reduction vary with respect to the combustion processes considered.
Perform the initial simulation with the respective conditions (Temperature, Pressure, Composition) pertaining to the specific problem and its targets using the Initial Mechanism. This step will give us the reference curves of the problem, for example the Ignition Delay time for the initial mechanism.
Then with the reference data in place, we will slowly reduce the mechanism to fit our problem parameters. This step is achieved by performing the respective sensitivity analysis and sorting the most sensitive reactions in the mechanisms.
The sorted mechanisms in the second step are converted into a separate mechanism file and the same simulation is performed from the first step but, this time with the reduced mechanism.
For the current case, we are trying to reduce the mechanism with respect to the reference Maximum Temperature and Ignition Delay time.
The project entails a Python program which performs a chemical reaction mechanism reduction using the Cantera library. This is an introductory code on reduction and its effects on different cases.
It does the following:
- Parses Reduction Parameters: It reads reduction parameters like temperature, pressure, and equivalence ratio from a file
Reduction_Parameters.txt, storing these in a dictionary. - Simulates Ignition Delay and Temperature: For different initial conditions (temperature, pressure, and fuel mixture), it sets up a constant pressure reactor to simulate the ignition process, calculates the ignition delay (time it takes for a significant temperature rise), and records the maximum temperature.
- Sensitivity Analysis: The program uses sensitivity analysis for reactions in the mechanism to determine their importance.
- Mechanism Reduction: It removes unimportant reactions to create a reduced chemical mechanism and reruns the simulation with this reduced mechanism.
- Plots Results: It generates and saves plots comparing ignition delay and maximum temperature against the number of reactions for each test case.
Results and Observations
The resulting test cases results and data is given below:
Case 1 (950K, 3 bar, 0.5 Equivalence Ratio)
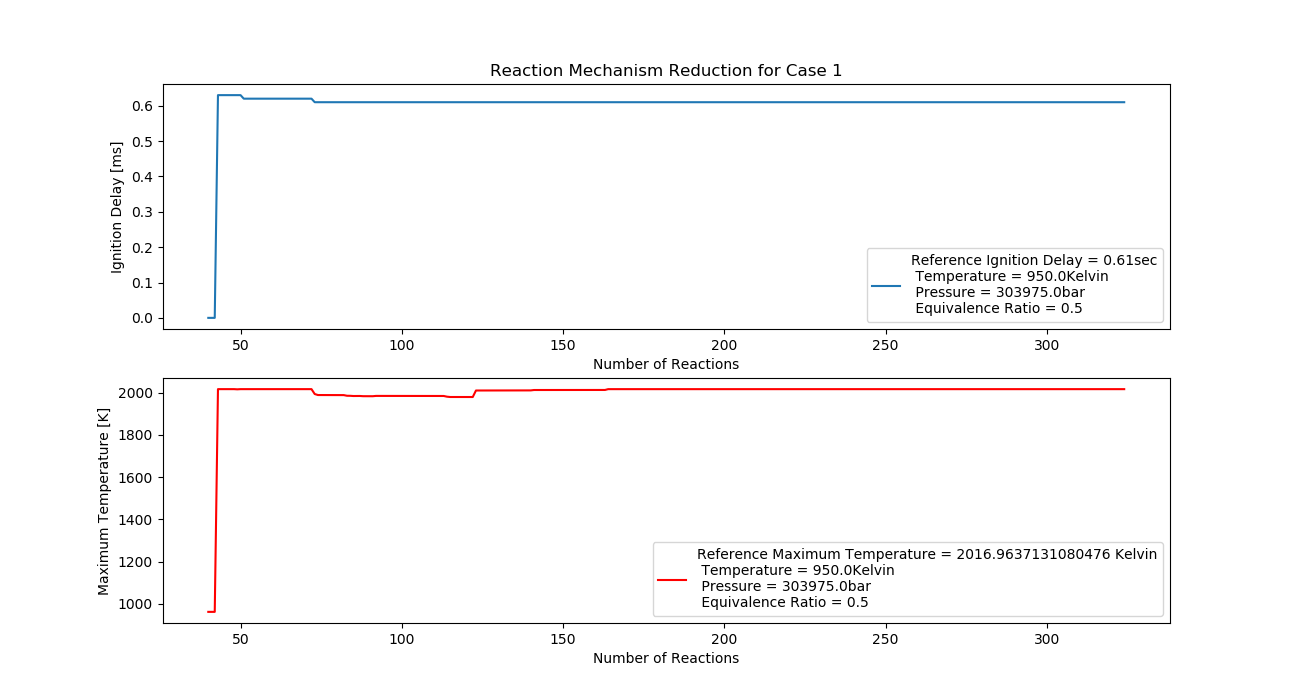
- Ignition Delay: 0.072 ms with 72 reactions.
- Max Temperature: 1630K with 163 reactions.
- Observation: Efficient combustion with a low ignition delay and stable temperature.
Case 2 (950K, 3 bar, 1 Equivalence Ratio)
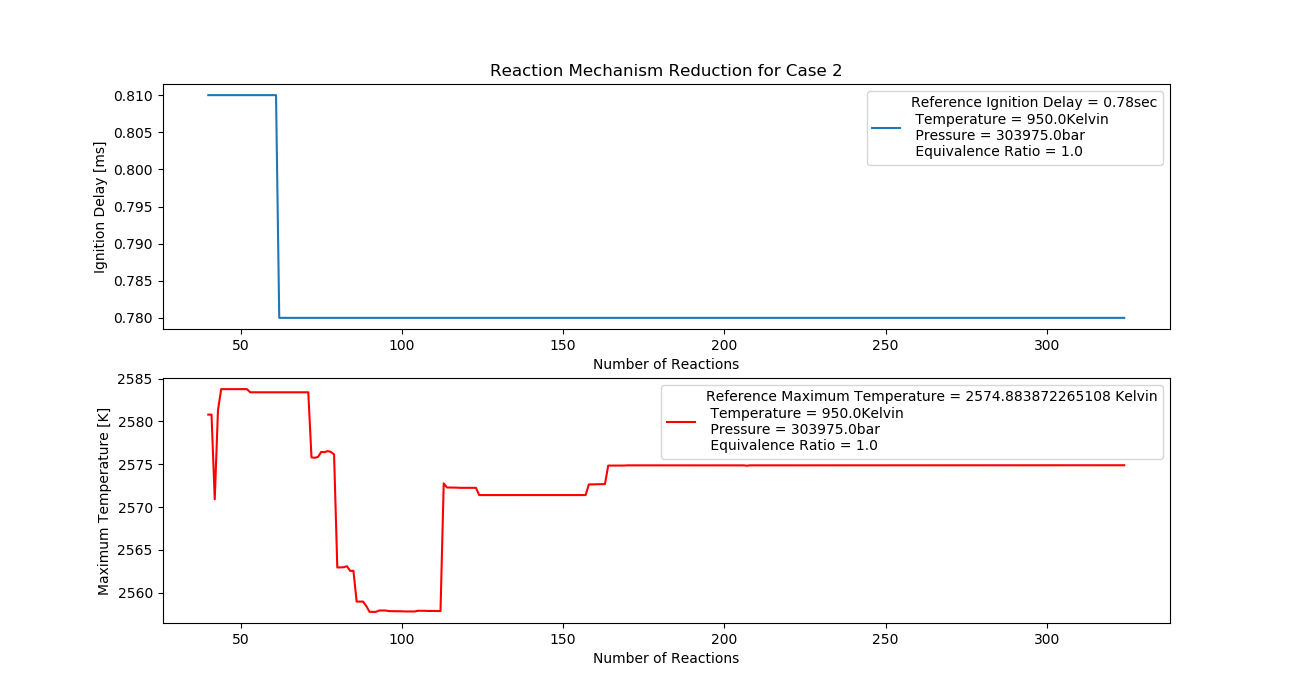
- Ignition Delay: 0.062 ms with 62 reactions.
- Max Temperature: 1640K with 164 reactions.
- Observation: Stoichiometric mix improves ignition delay and temperature stability.
Case 3 (950K, 3 bar, 1.5 Equivalence Ratio)
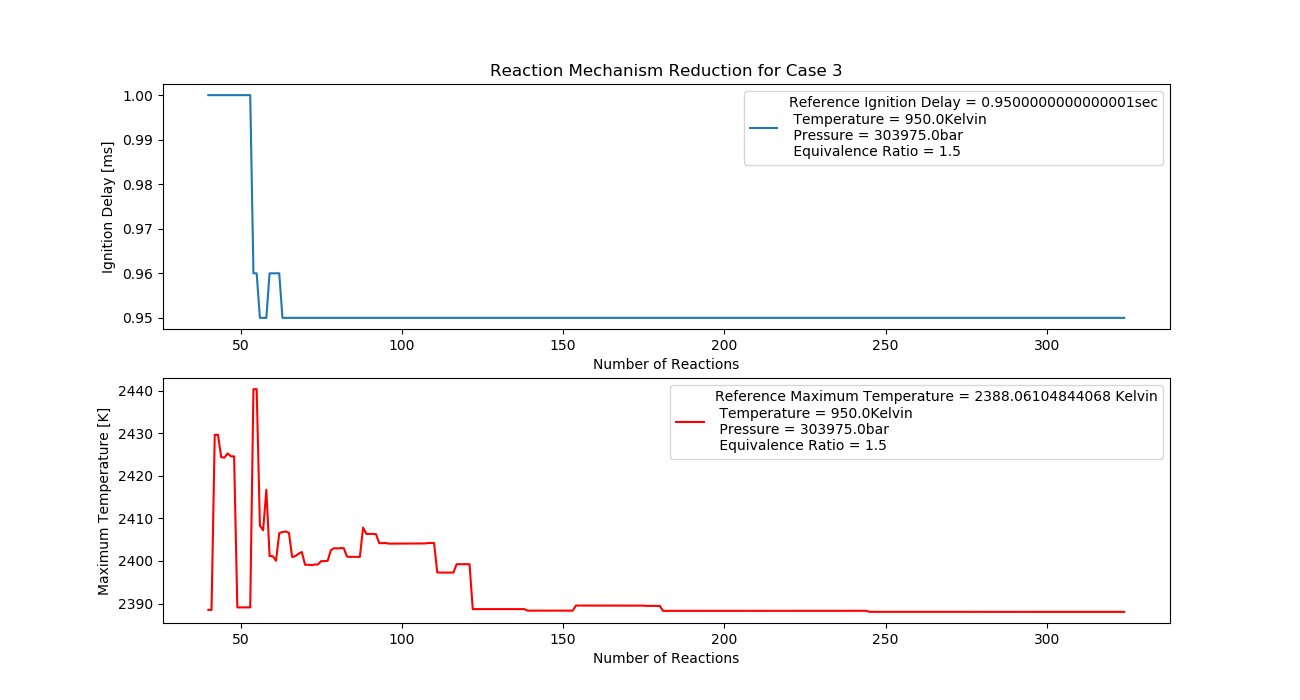
- Ignition Delay: 0.063 ms with 63 reactions.
- Max Temperature: 2450K with 245 reactions.
- Observation: Fuel-rich mix results in a significant temperature increase.
Case 4 (950K, 4 bar, 0.5 Equivalence Ratio)
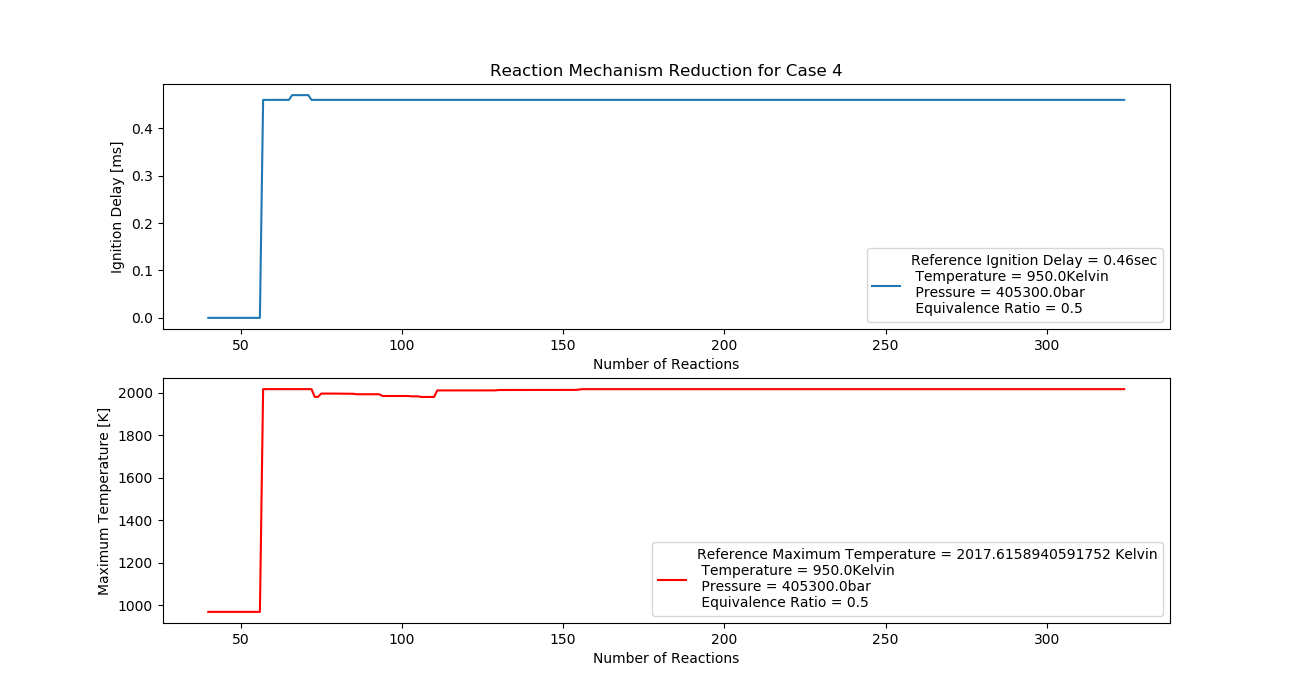
- Ignition Delay: 0.071 ms with 71 reactions.
- Max Temperature: 1550K with 155 reactions.
- Observation: Higher pressure slightly reduces the maximum temperature.
Case 5 (950K, 4 bar, 1 Equivalence Ratio)
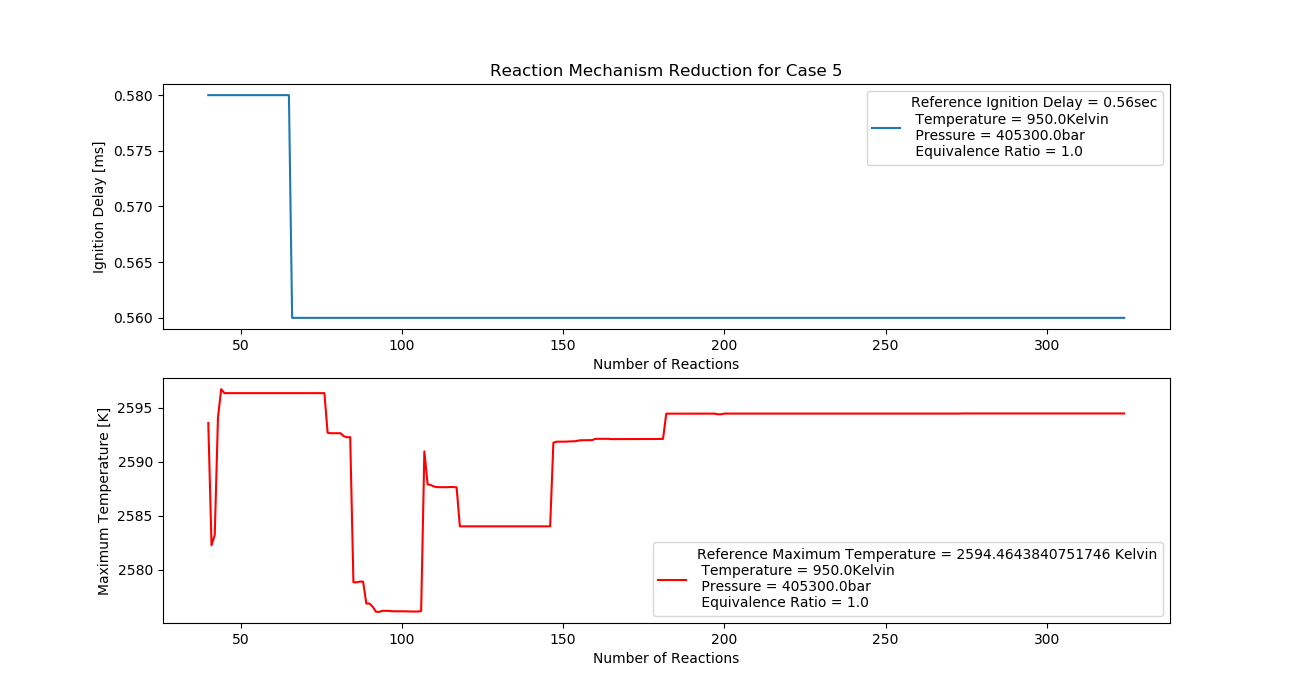
- Ignition Delay: 0.065 ms with 65 reactions.
- Max Temperature: 1990K with 199 reactions.
- Observation: Higher pressure increases the temperature stability.
Case 6 (950K, 4 bar, 1.5 Equivalence Ratio)
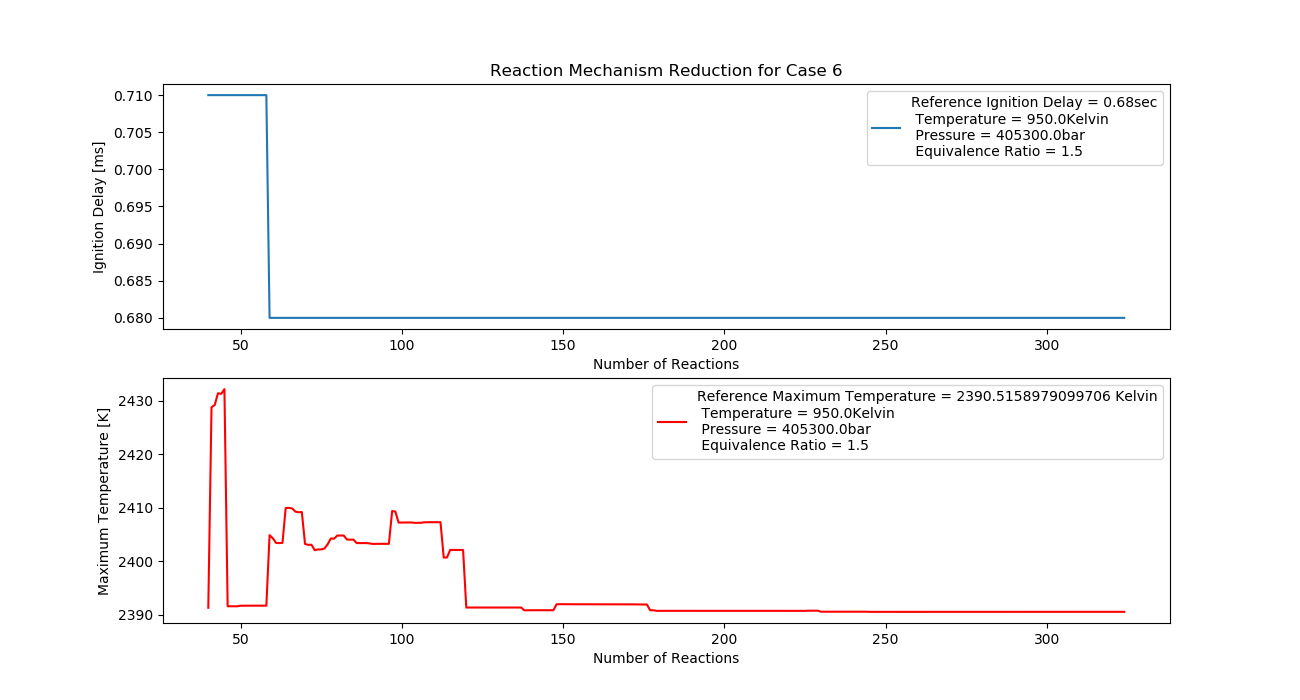
- Ignition Delay: 0.058 ms with 58 reactions.
- Max Temperature: 2300K with 230 reactions.
- Observation: High equivalence ratio and pressure increase temperature.
Case 7 (950K, 5 bar, 0.5 Equivalence Ratio)
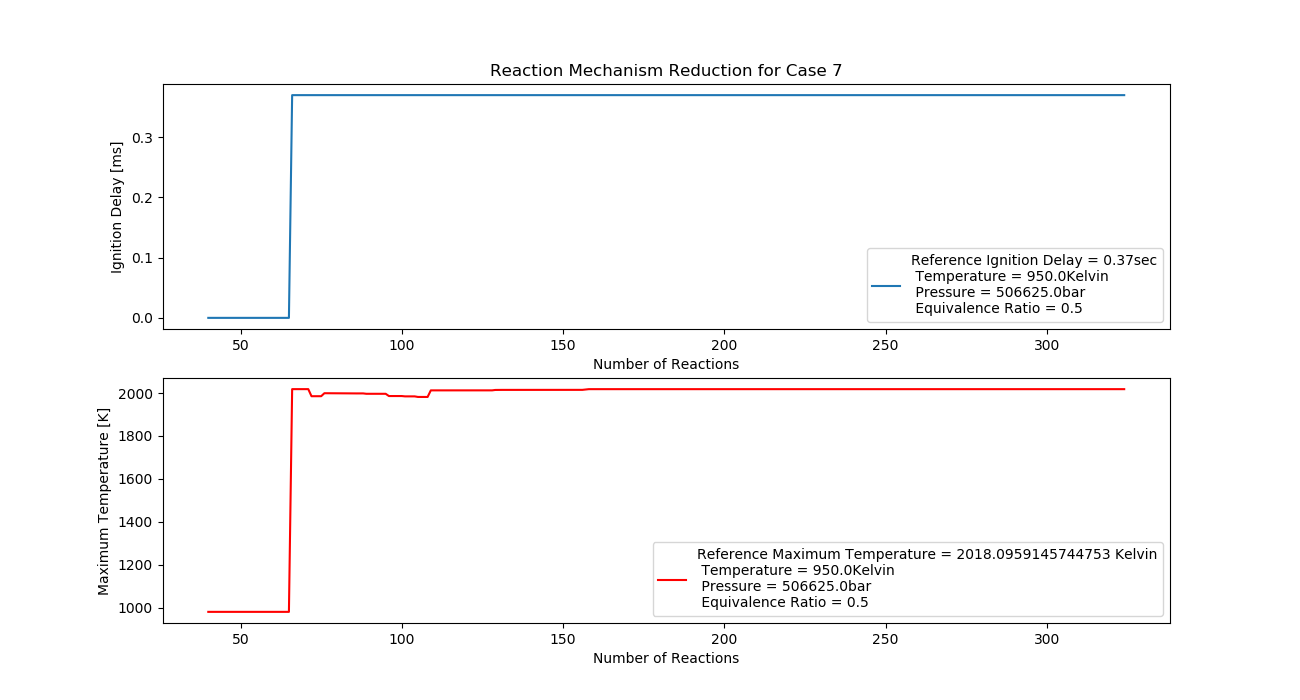
- Ignition Delay: 0.065 ms with 65 reactions.
- Max Temperature: 1570K with 157 reactions.
- Observation: Increasing pressure lowers temperature compared to richer mixtures.
Case 8 (950K, 5 bar, 1 Equivalence Ratio)
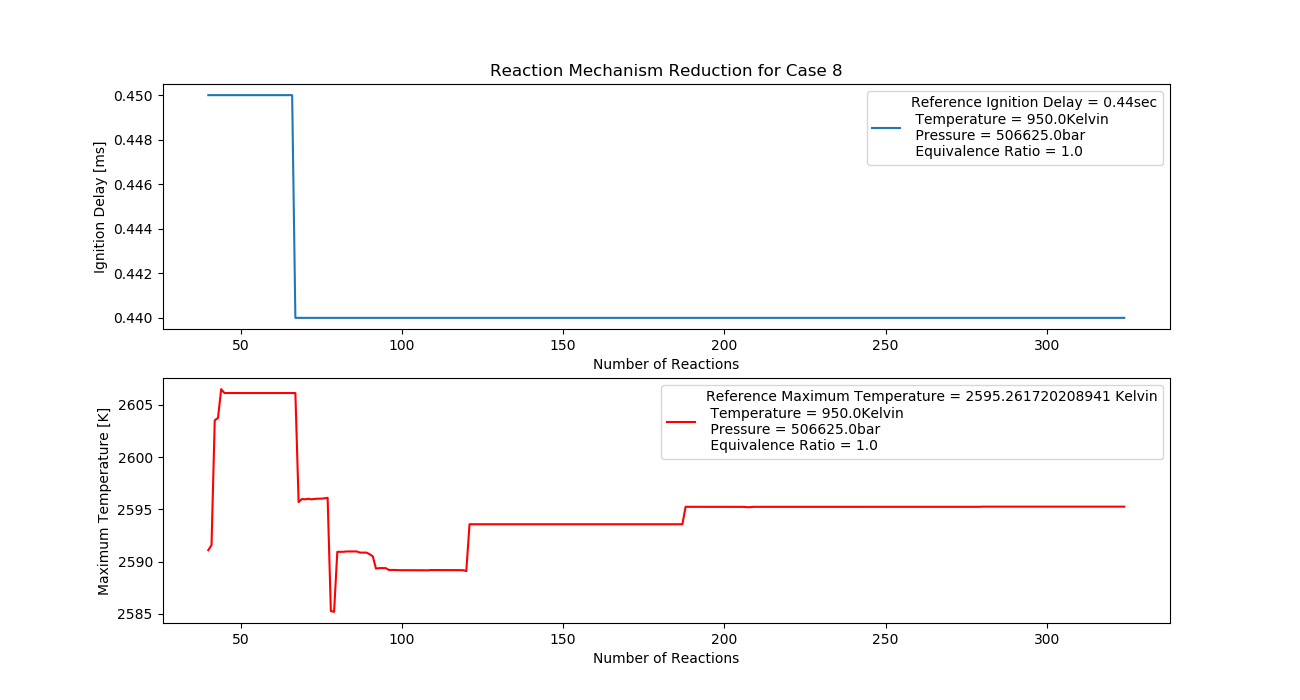
- Ignition Delay: 0.067 ms with 67 reactions.
- Max Temperature: 2080K with 208 reactions.
- Observation: Higher pressure increases temperature stability.
Case 9 (950K, 5 bar, 1.5 Equivalence Ratio)
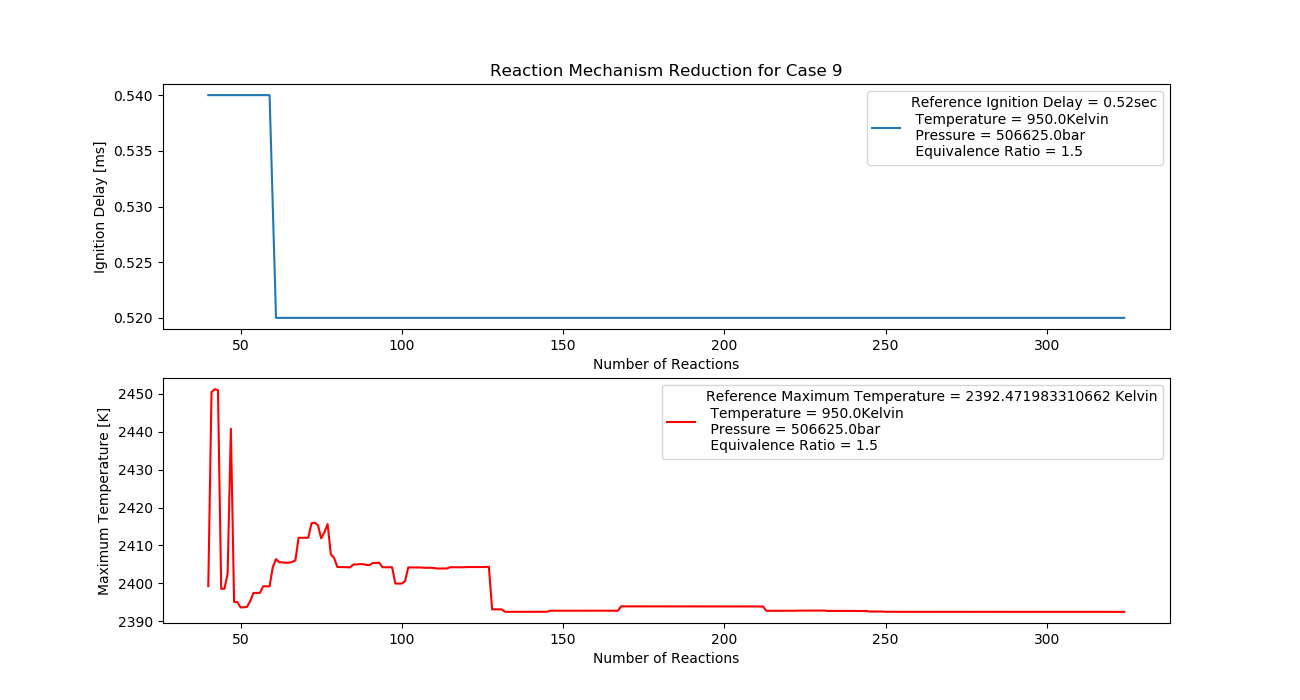
- Ignition Delay: 0.060 ms with 60 reactions.
- Max Temperature: 2440K with 244 reactions.
- Observation: Rich fuel at high pressure yields high temperatures.
Case 10 (1050K, 3 bar, 0.5 Equivalence Ratio)
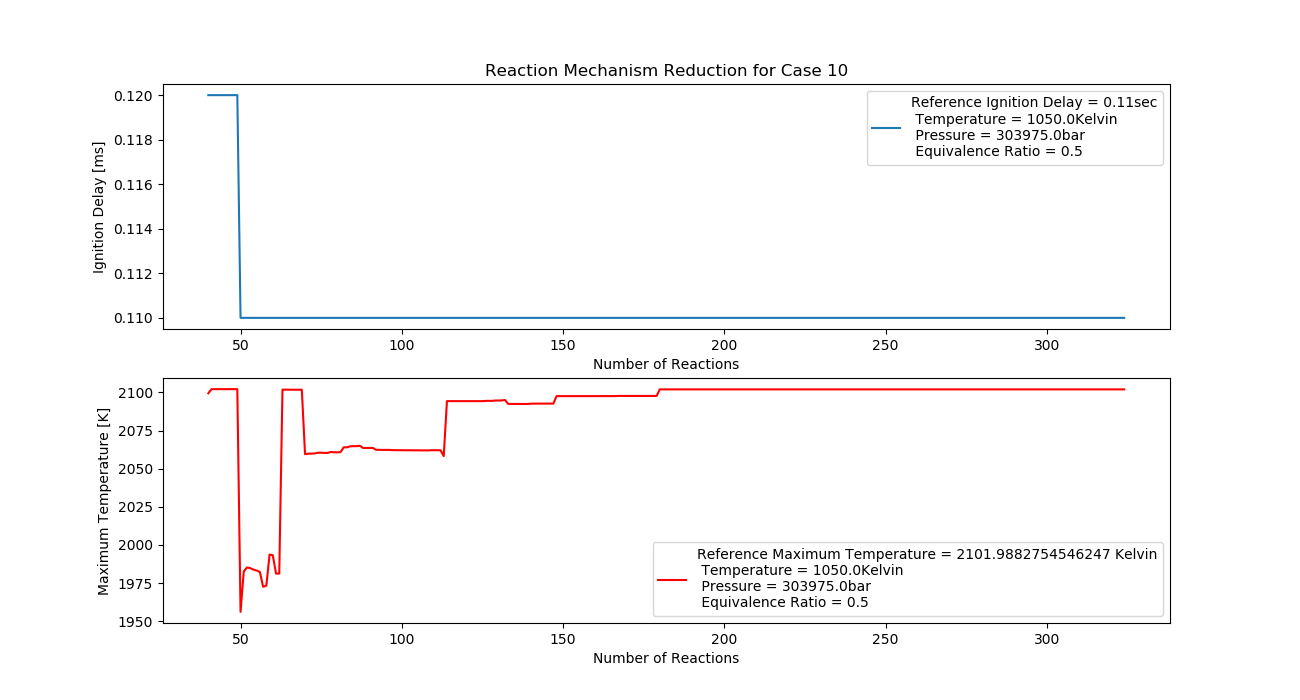
- Ignition Delay: 0.049 ms with 49 reactions.
- Max Temperature: 1800K with 180 reactions.
- Observation: Increased temperature improves ignition efficiency.
Case 11 (1050K, 3 bar, 1 Equivalence Ratio)
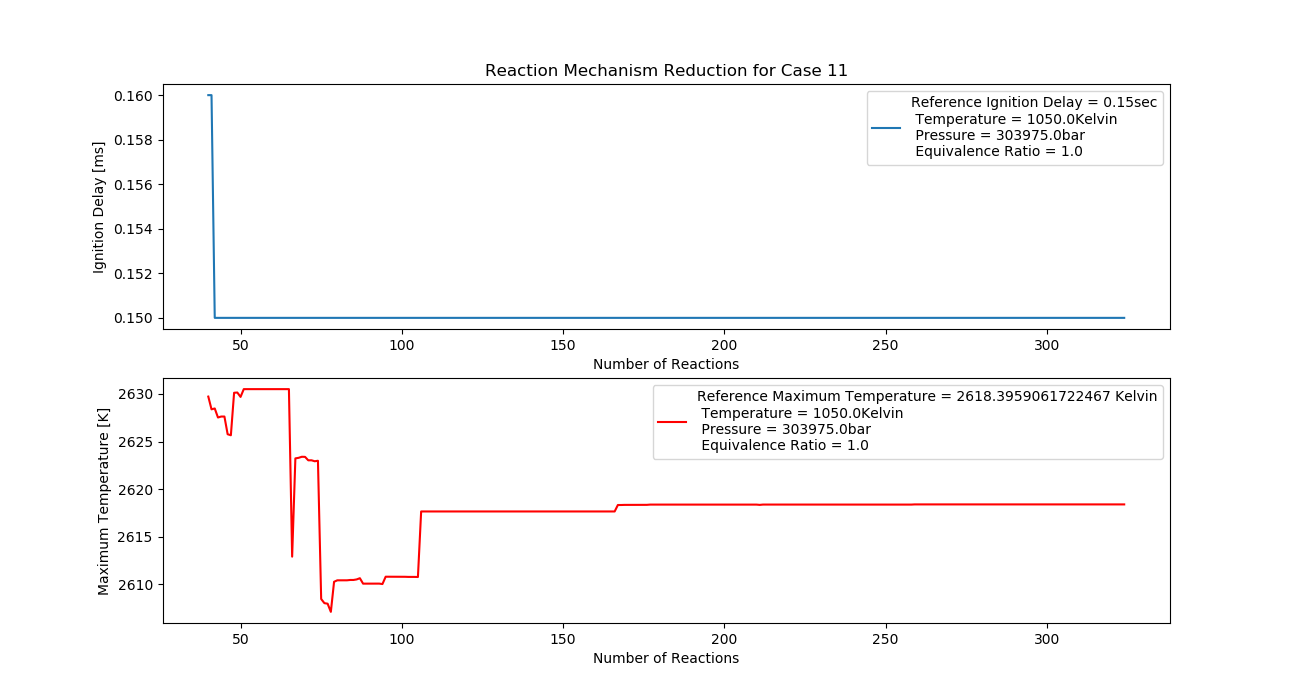
- Ignition Delay: 0.043 ms with 43 reactions.
- Max Temperature: 1670K with 167 reactions.
- Observation: Lower ignition delay with a stoichiometric mix.
Case 12 (1050K, 3 bar, 1.5 Equivalence Ratio)
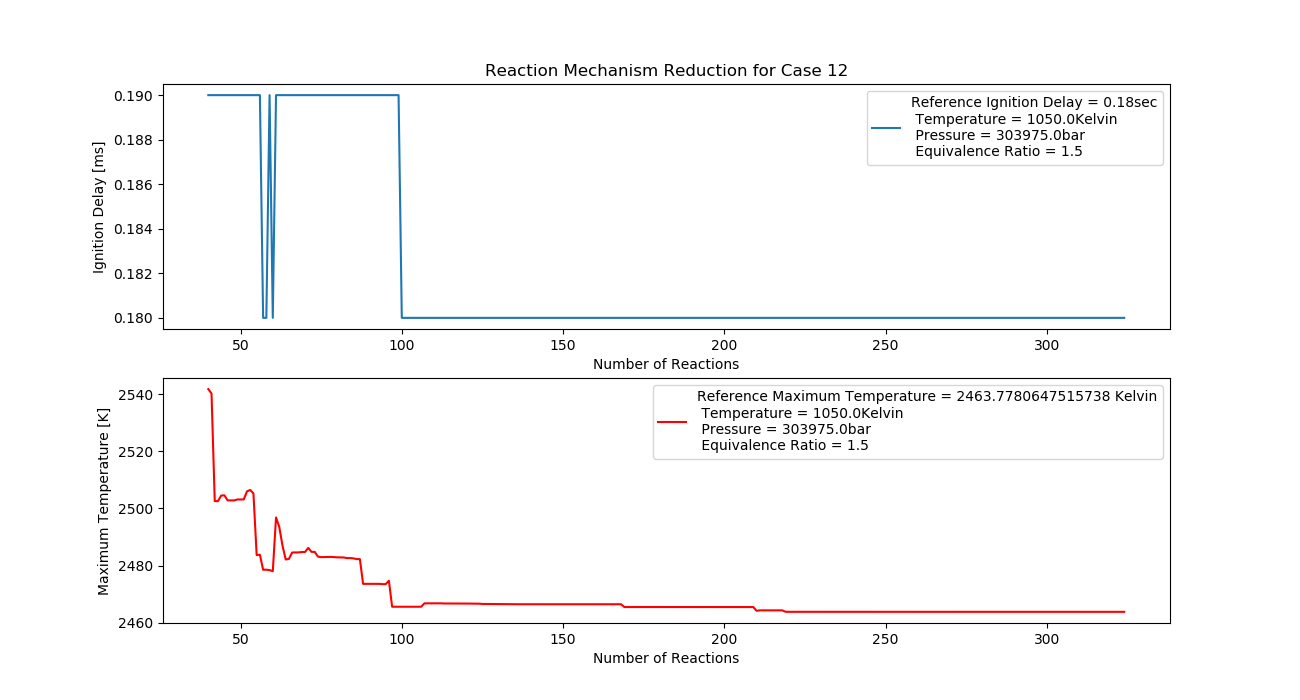
- Ignition Delay: 0.099 ms with 99 reactions.
- Max Temperature: 2180K with 218 reactions.
- Observation: Fuel-rich conditions cause incomplete combustion and higher temperatures.
Case 13 (1050K, 4 bar, 0.5 Equivalence Ratio)
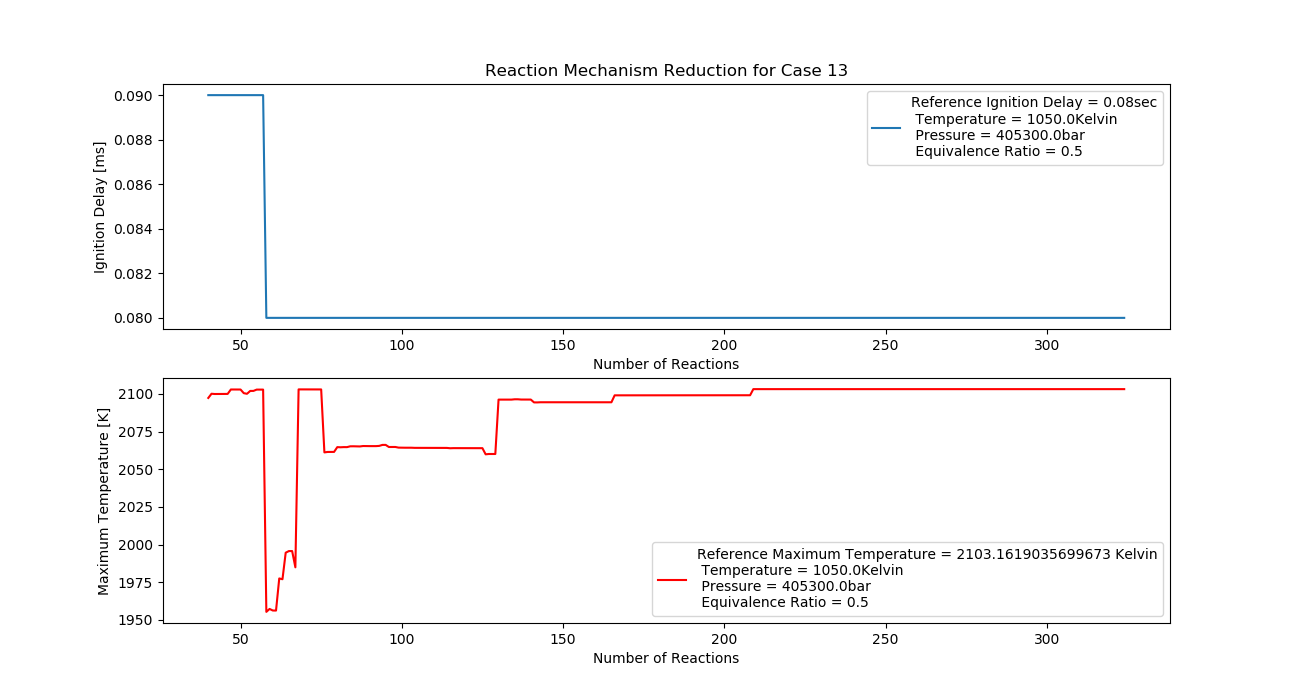
- Ignition Delay: 0.057 ms with 57 reactions.
- Max Temperature: 2080K with 208 reactions.
- Observation: Higher pressure improves combustion efficiency.
Case 14 (1050K, 4 bar, 1 Equivalence Ratio)
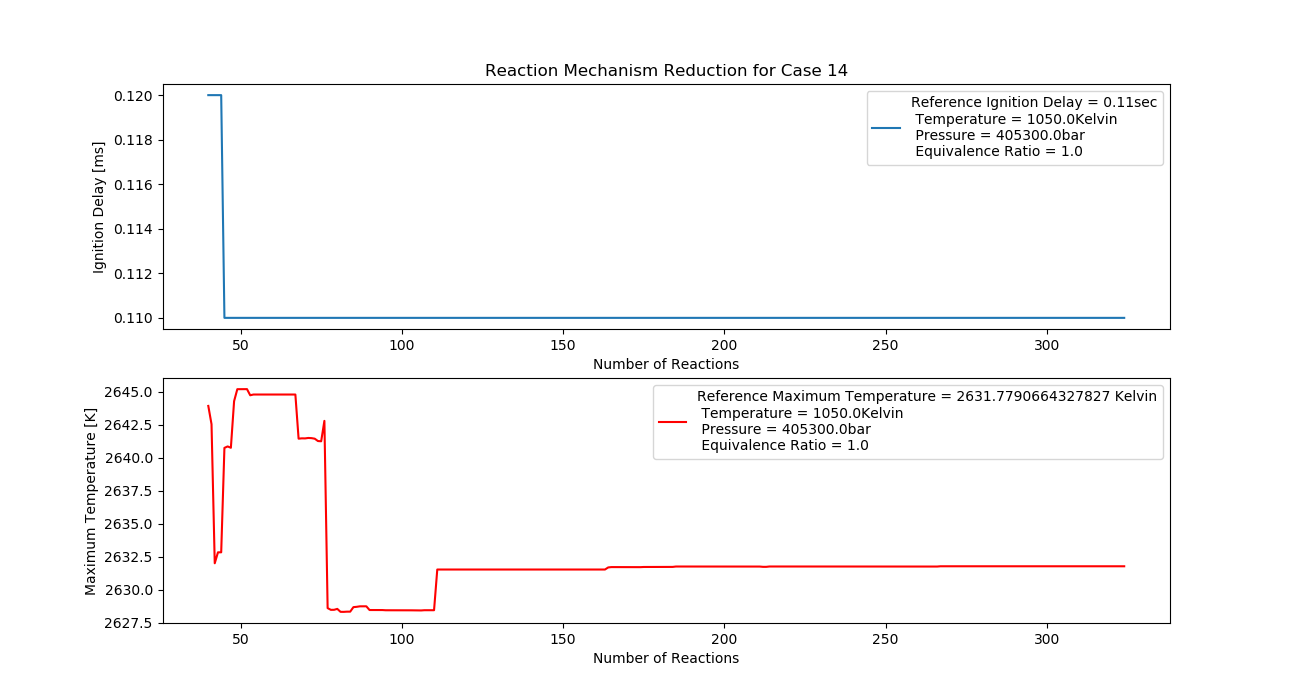
- Ignition Delay: 0.044 ms with 44 reactions.
- Max Temperature: 1640K with 164 reactions.
- Observation: Stoichiometric mix provides stable temperature.
Case 15 (1050K, 4 bar, 1.5 Equivalence Ratio)
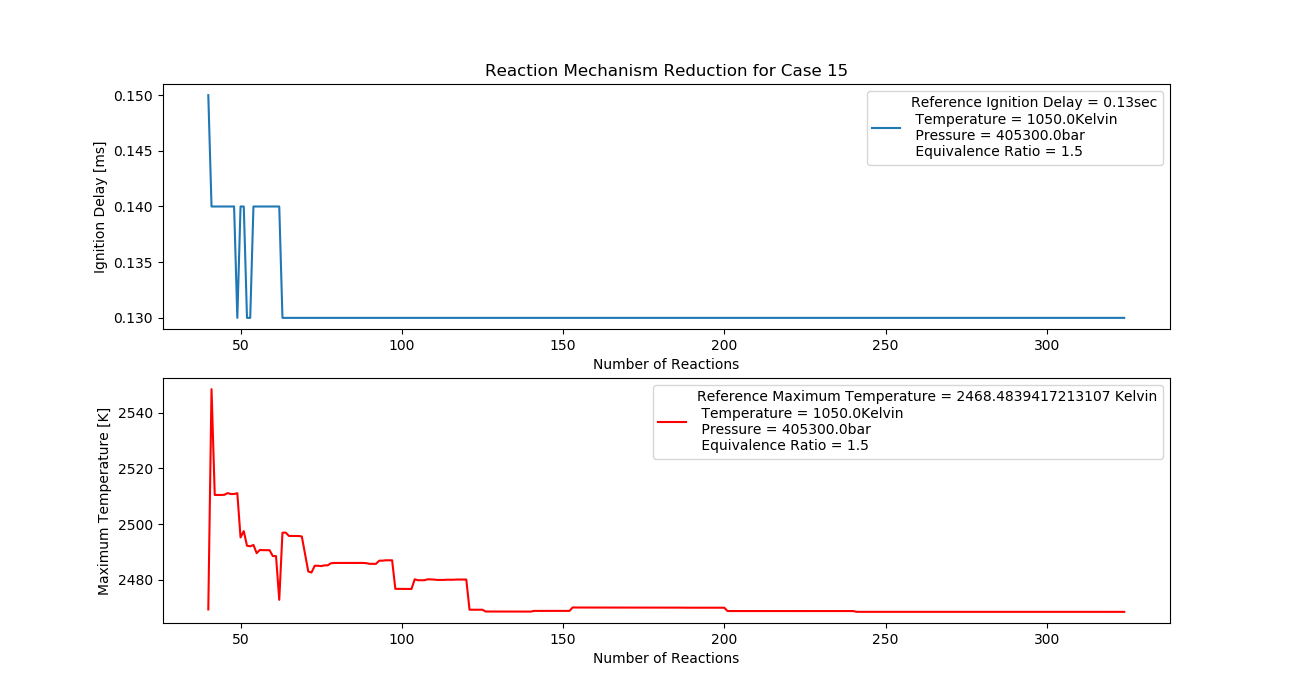
- Ignition Delay: 0.063 ms with 63 reactions.
- Max Temperature: 2400K with 240 reactions.
- Observation: Fuel-rich conditions lead to higher temperatures.
Case 16 (1050K, 5 bar, 0.5 Equivalence Ratio)
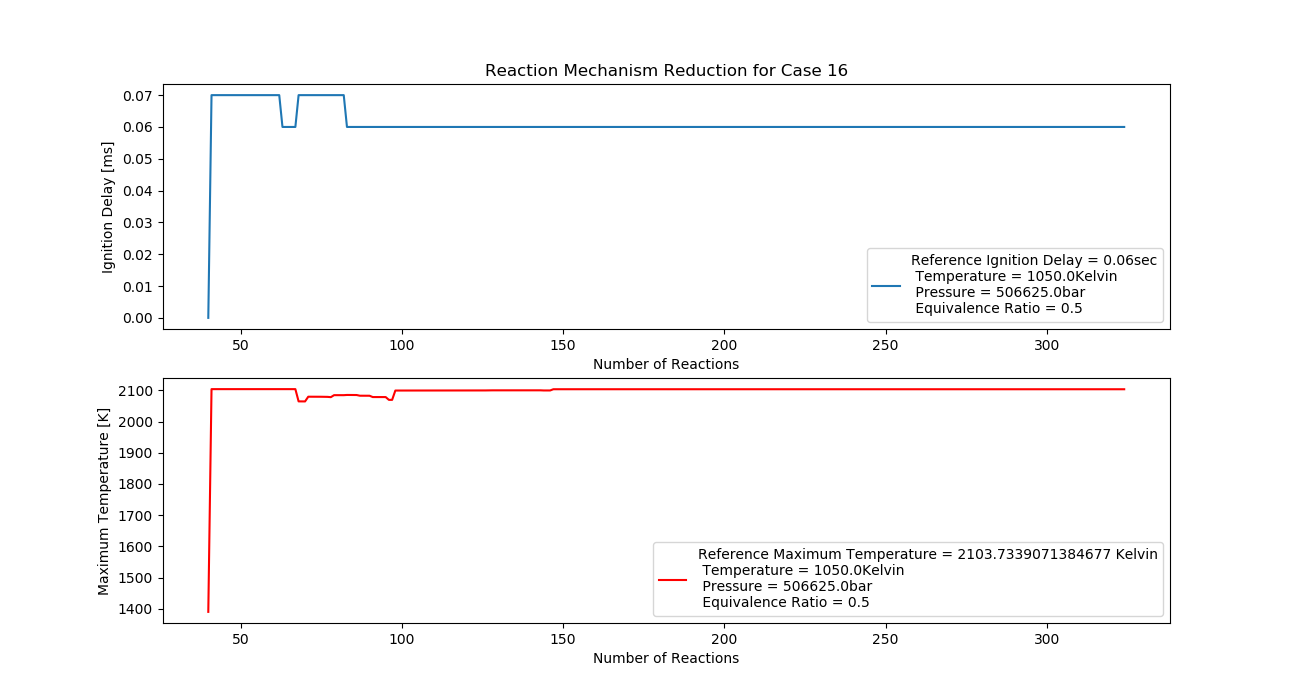
- Ignition Delay: 0.083 ms with 83 reactions.
- Max Temperature: 1470K with 147 reactions.
- Observation: Lean mixture and high pressure reduce temperature.
Case 17 (1050K, 5 bar, 1 Equivalence Ratio)
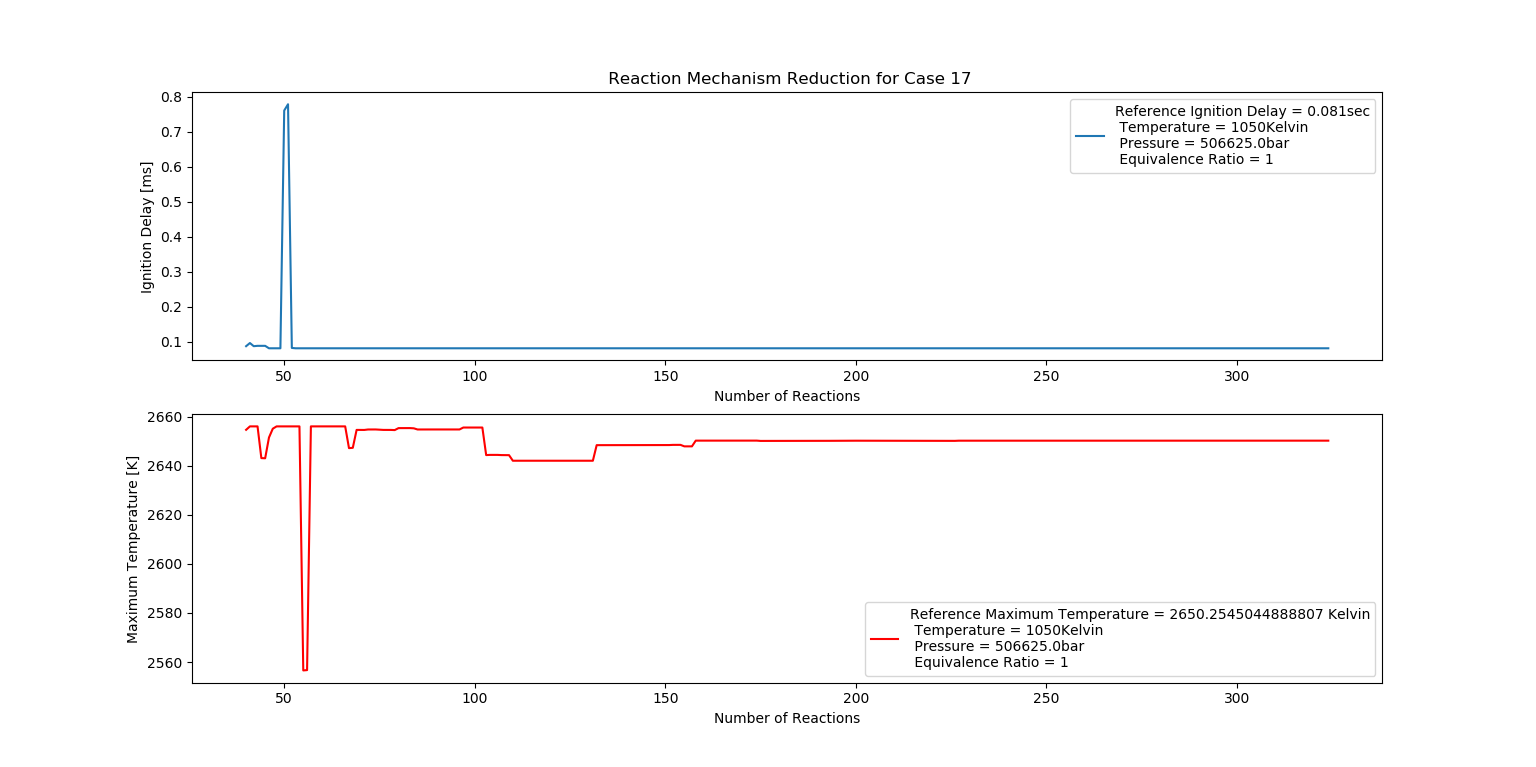
- Ignition Delay: 0.052 ms with 52 reactions.
- Max Temperature: 1580K with 158 reactions.
- Observation: Stoichiometric mix provides stable combustion.
Case 18 (1050K, 5 bar, 1.5 Equivalence Ratio)
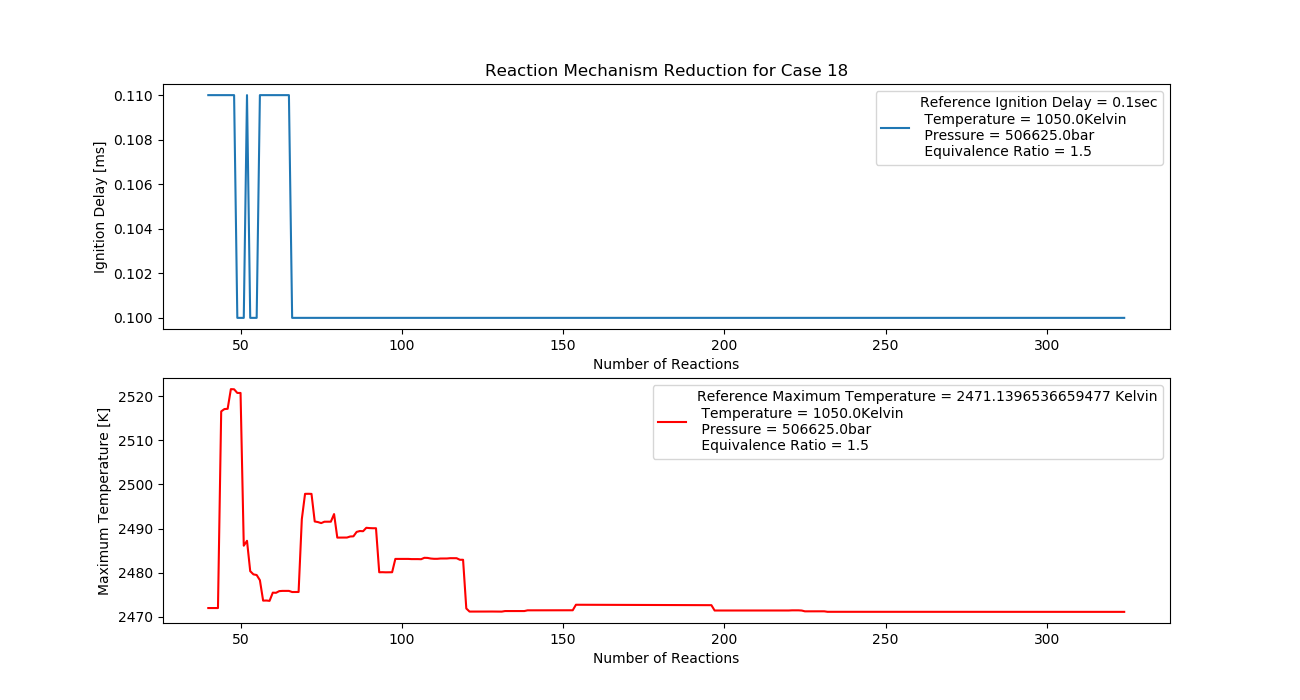
- Ignition Delay: 0.065 ms with 65 reactions.
- Max Temperature: 2310K with 231 reactions.
- Observation: Rich fuel and high pressure generate high temperatures.
Case 19 (1150K, 3 bar, 0.5 Equivalence Ratio)
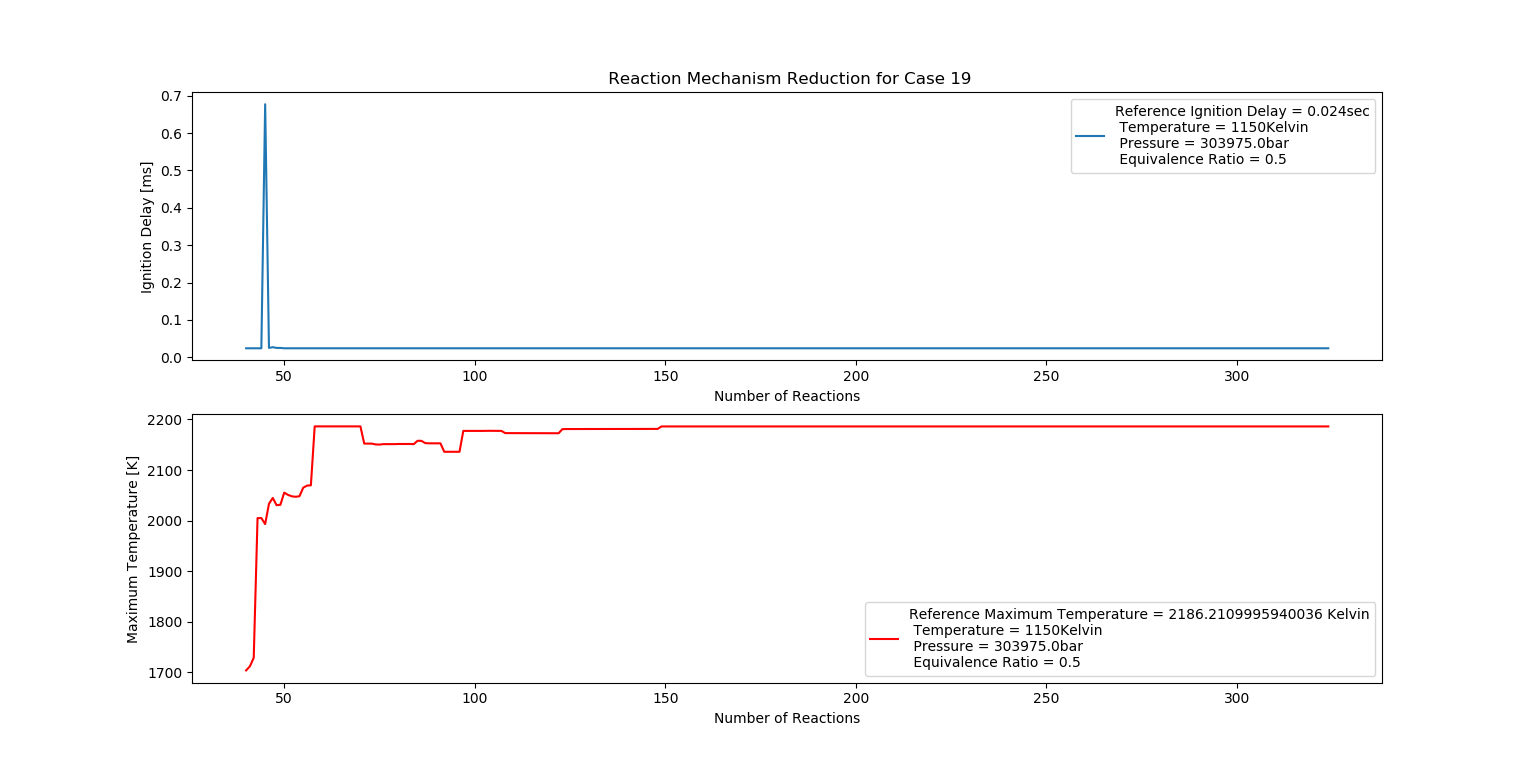
- Ignition Delay: 0.050 ms with 50 reactions.
- Max Temperature: 1490K with 149 reactions.
- Observation: Increased temperature results in efficient combustion.
Case 20 (1150K, 3 bar, 1 Equivalence Ratio)
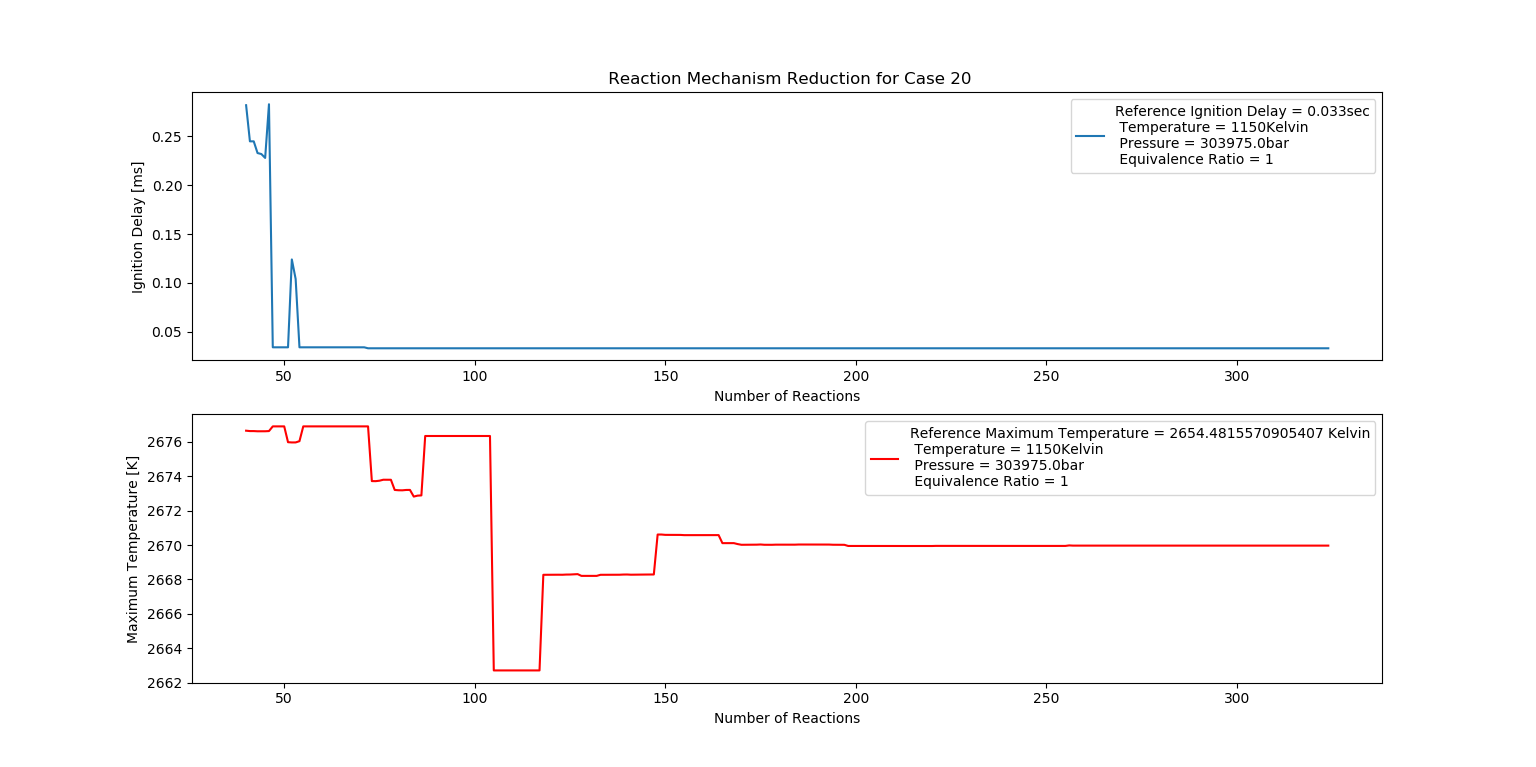
- Ignition Delay: 0.072 ms with 72 reactions.
- Max Temperature: 2570K with 257 reactions.
- Observation: Stoichiometric conditions produce very high temperatures.
Case 21 (1150K, 3 bar, 1.5 Equivalence Ratio)
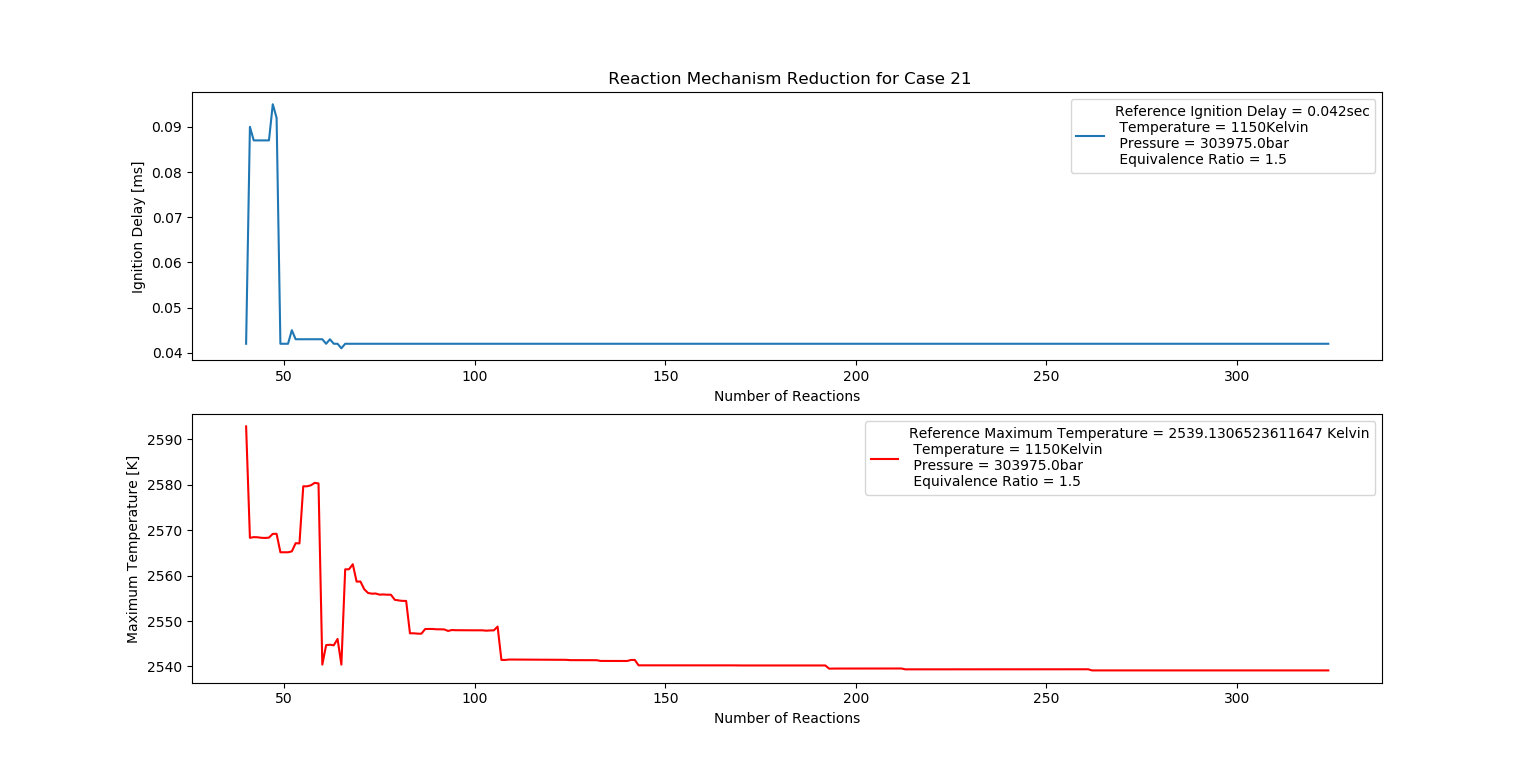
- Ignition Delay: 0.066 ms with 66 reactions.
- Max Temperature: 2620K with 262 reactions.
- Observation: Rich fuel and high temperature lead to combustion instability.
Case 22 (1150K, 4 bar, 0.5 Equivalence Ratio)
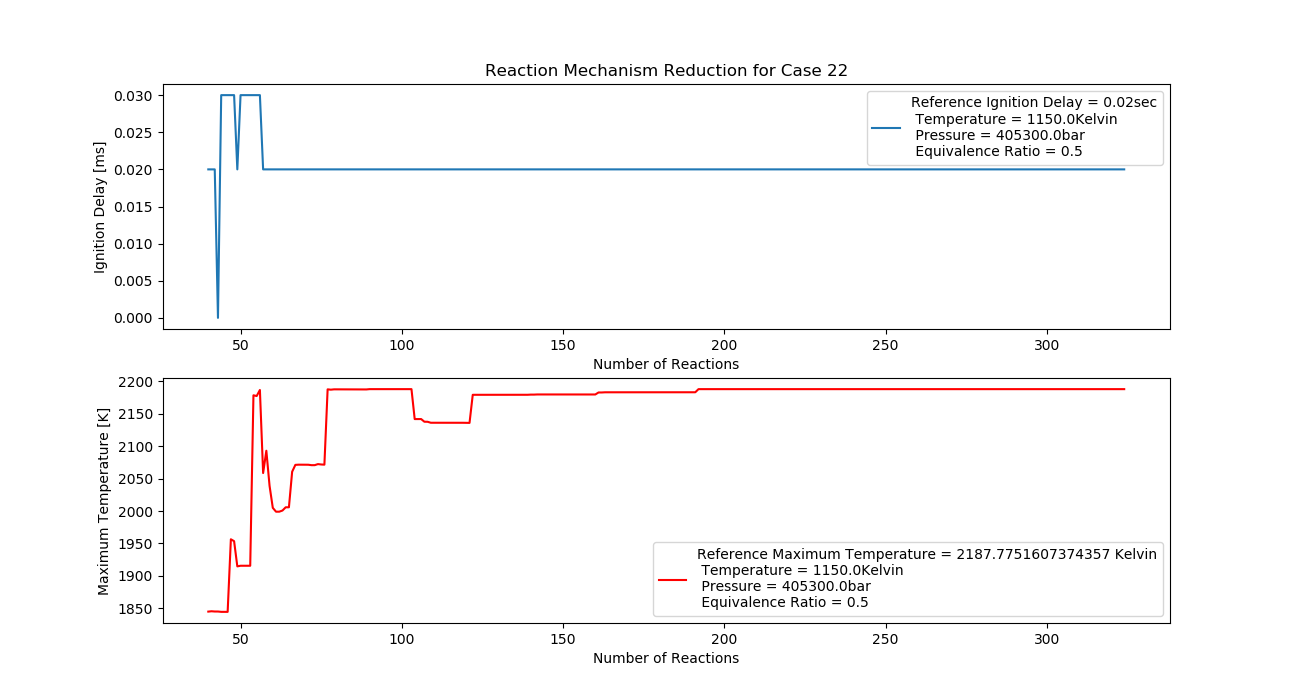
- Ignition Delay: 0.057 ms with 57 reactions.
- Max Temperature: 1920K with 192 reactions.
- Observation: Lean mixture and high pressure reduce temperature.
Case 23 (1150K, 4 bar, 1 Equivalence Ratio)
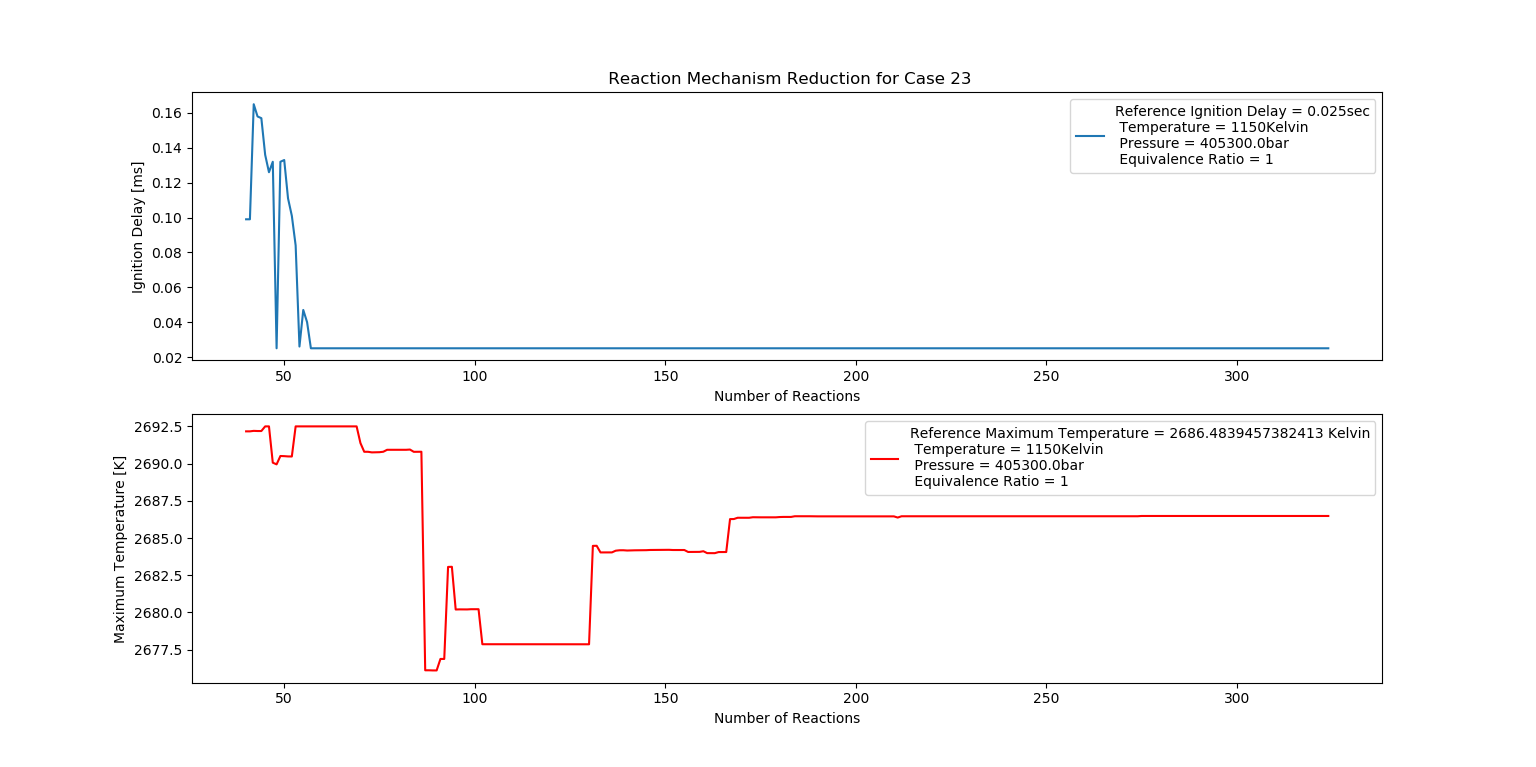
- Ignition Delay: 0.057 ms with 57 reactions.
- Max Temperature: 2120K with 212 reactions.
- Observation: Stoichiometric conditions result in stable combustion.
Case 24 (1150K, 4 bar, 1.5 Equivalence Ratio)
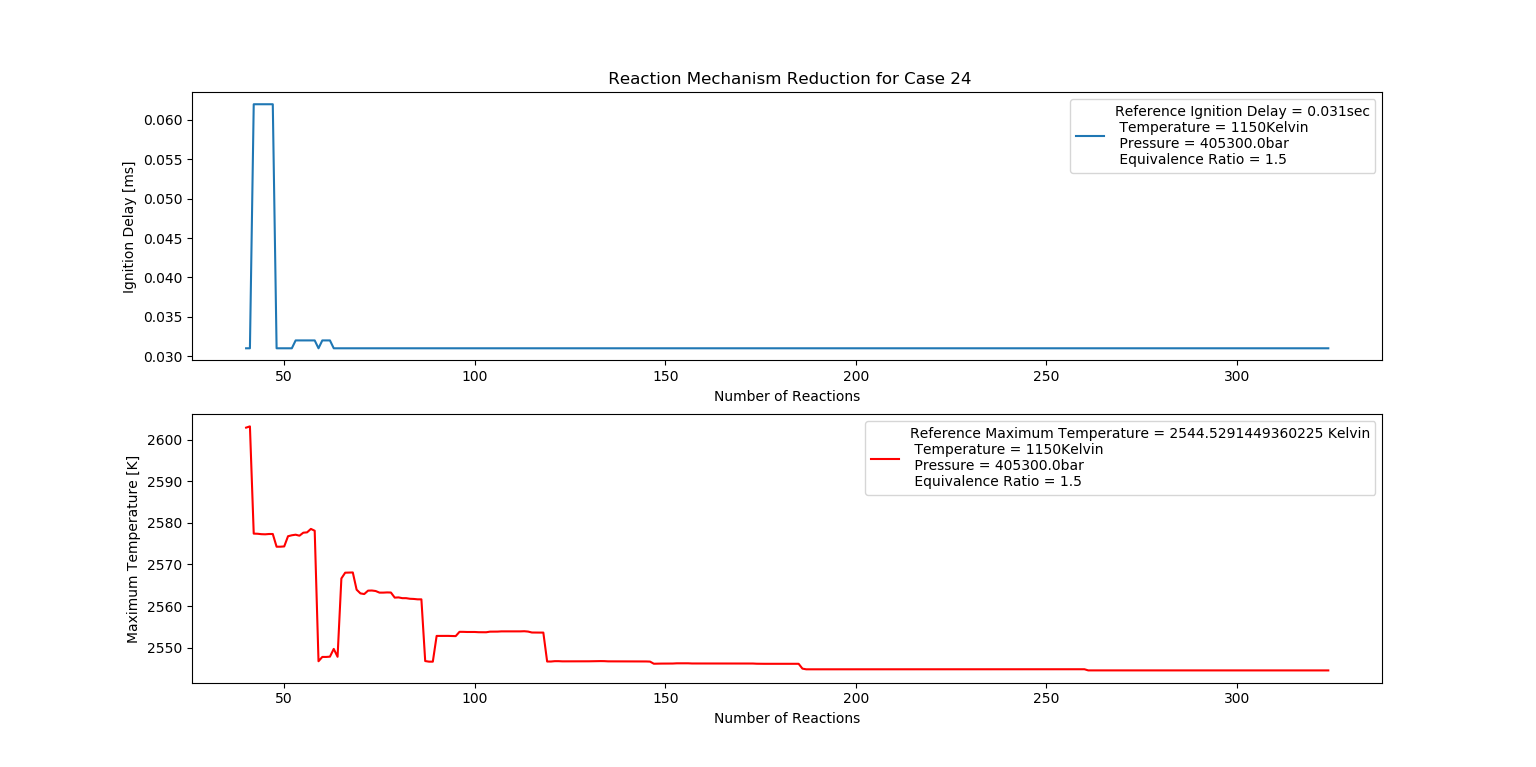
- Ignition Delay: 0.063 ms with 63 reactions.
- Max Temperature: 2610K with 261 reactions.
- Observation: Rich fuel mixture increases combustion temperature.
Case 25 (1150K, 5 bar, 0.5 Equivalence Ratio)
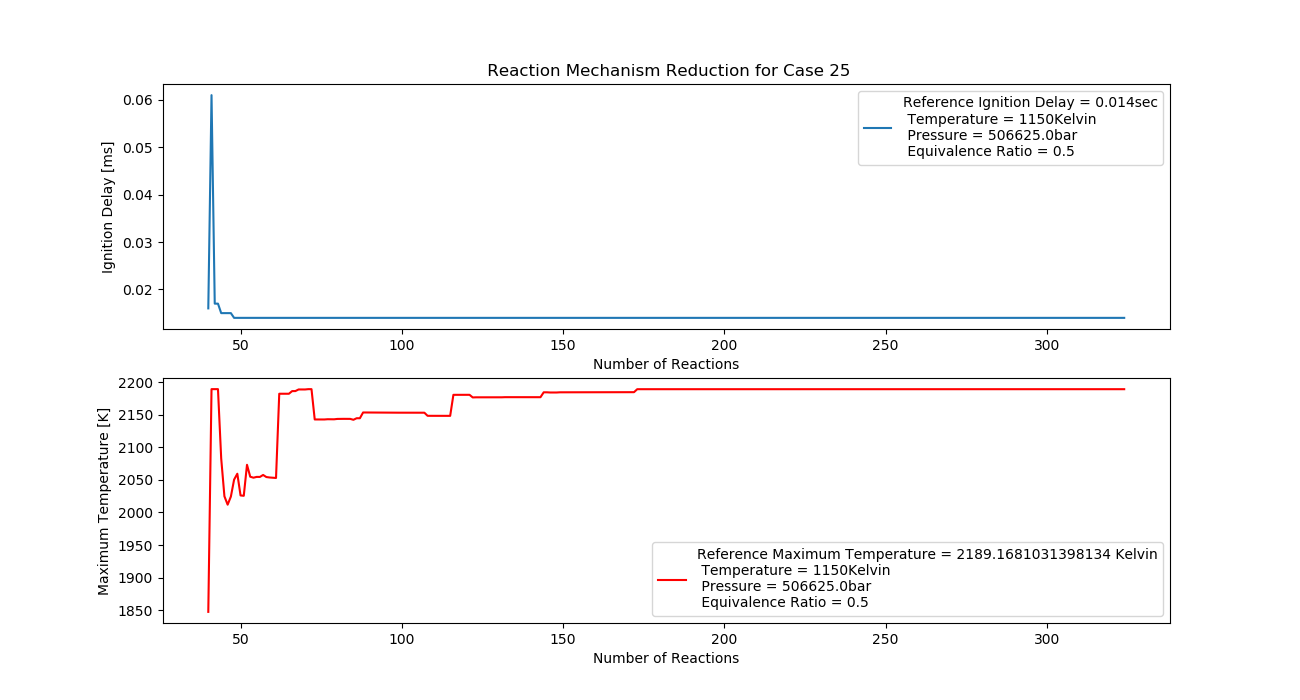
- Ignition Delay: 0.048 ms with 48 reactions.
- Max Temperature: 1730K with 173 reactions.
- Observation: Lean fuel reduces ignition delay and temperature.
Case 26 (1150K, 5 bar, 1 Equivalence Ratio)
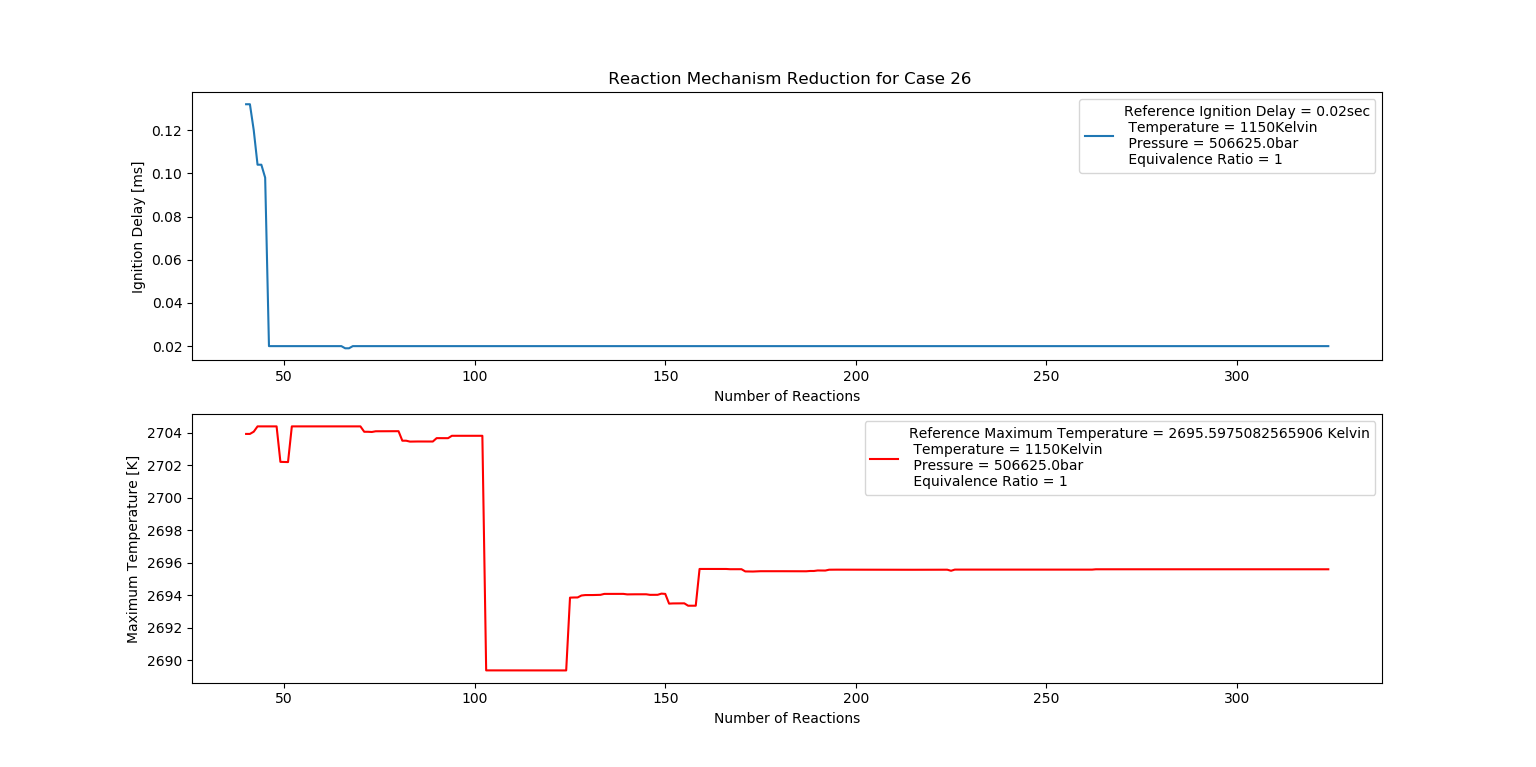
- Ignition Delay: 0.068 ms with 68 reactions.
- Max Temperature: 2260K with 226 reactions.
- Observation: Stoichiometric mix produces efficient combustion.
Case 27 (1150K, 5 bar, 1.5 Equivalence Ratio)
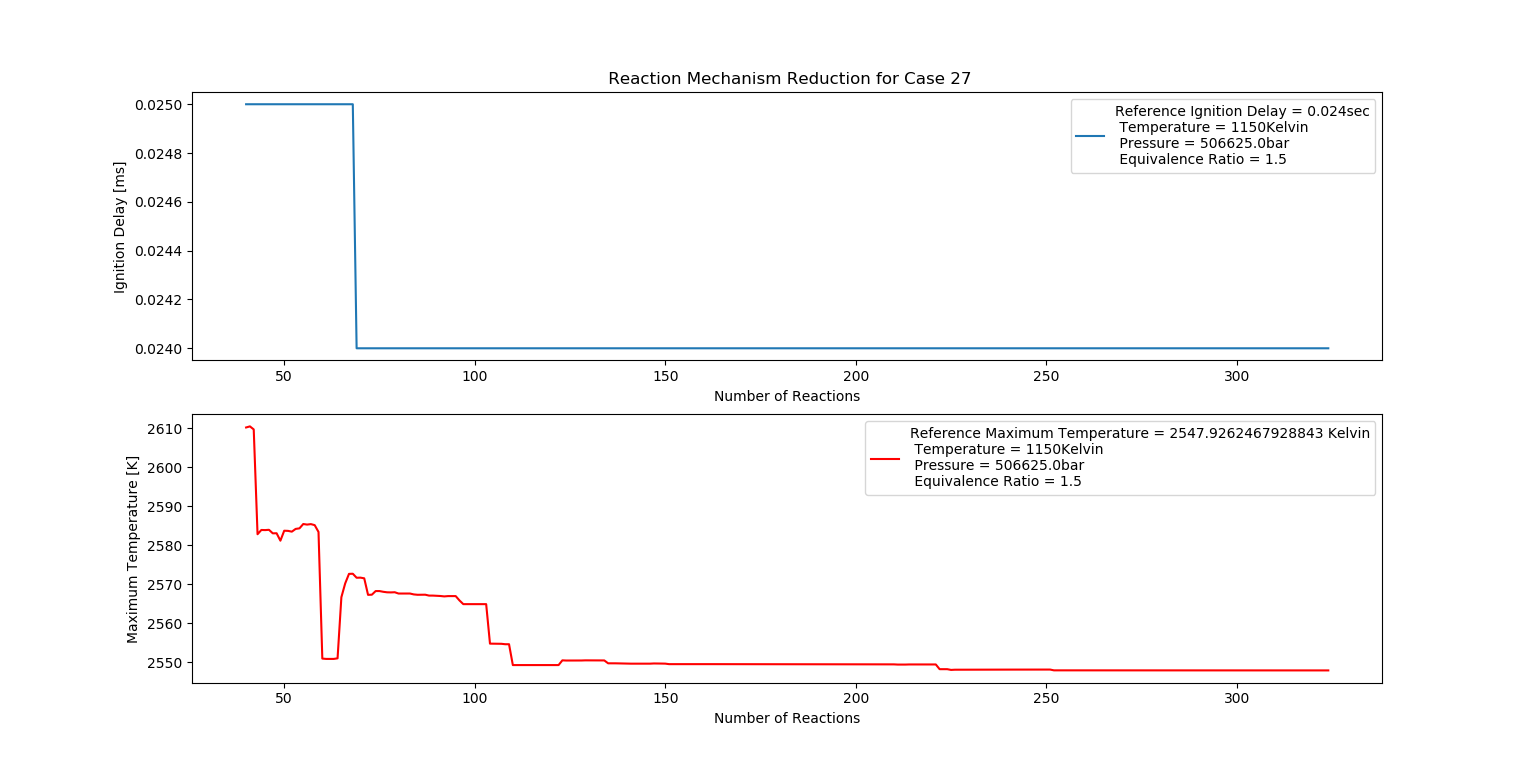
- Ignition Delay: 0.069 ms with 69 reactions.
- Max Temperature: 2520K with 252 reactions.
- Observation: Rich fuel mix increases temperature but may cause instability.
The factors that influence Ignition Delay:
We have established for the Auto Ignition challenge that Ignition Delay is sensitive to an increase in Temperature and pressure and it can be corroborated in the above cases. Keeping the former statement in consideration, we can also establish that the Equivalence ratio has a higher contribution to the Ignition Delay which can also be corroborated from the above observations.
The nature of the reaction processes also contributes to the Ignition Delay i.e. the reactions’ nature being Endothermic or Exothermic.
The following table shows the Reduced Mechanisms for the above cases pertaining to Ignition Delay and Maximum Temperature:
| Case number | Temperature (Kelvin) | Pressure (Bar) | Equivalence Ratio (No Units) | Reduced mechanism for Ignition Delay (Number of reactions) | Reduced mechanism for Maximum Temperature (Number of reactions) |
|---|---|---|---|---|---|
| 1 | 950 | 3 | 0.5 | 72 | 163 |
| 2 | 950 | 3 | 1 | 62 | 164 |
| 3 | 950 | 3 | 1.5 | 63 | 245 |
| 4 | 950 | 4 | 0.5 | 71 | 155 |
| 5 | 950 | 4 | 1 | 65 | 199 |
| 6 | 950 | 4 | 1.5 | 58 | 230 |
| 7 | 950 | 5 | 0.5 | 65 | 157 |
| 8 | 950 | 5 | 1 | 67 | 208 |
| 9 | 950 | 5 | 1.5 | 60 | 244 |
| 10 | 1050 | 3 | 0.5 | 49 | 180 |
| 11 | 1050 | 3 | 1 | 43 | 167 |
| 12 | 1050 | 3 | 1.5 | 99 | 218 |
| 13 | 1050 | 4 | 0.5 | 57 | 208 |
| 14 | 1050 | 4 | 1 | 44 | 164 |
| 15 | 1050 | 4 | 1.5 | 63 | 240 |
| 16 | 1050 | 5 | 0.5 | 83 | 147 |
| 17 | 1050 | 5 | 1 | 52 | 158 |
| 18 | 1050 | 5 | 1.5 | 65 | 231 |
| 19 | 1150 | 3 | 0.5 | 50 | 149 |
| 20 | 1150 | 3 | 1 | 72 | 257 |
| 21 | 1150 | 3 | 1.5 | 66 | 262 |
| 22 | 1150 | 4 | 0.5 | 57 | 192 |
| 23 | 1150 | 4 | 1 | 57 | 212 |
| 24 | 1150 | 4 | 1.5 | 63 | 261 |
| 25 | 1150 | 5 | 0.5 | 48 | 173 |
| 26 | 1150 | 5 | 1 | 68 | 226 |
| 27 | 1150 | 5 | 1.5 | 69 | 252 |
The average Reduced Mechanism for the range of given state values contains around 60 to 65 reactions.
Note:
It is important to understand the trend we observe in the above images. For each step, we are finding the Ignition Delay and the Maximum Temperature for the previous mechanism with the addition of a new reaction. For example, a mechanism consisting of 40 reactions gives a specific value and the next mechanism with 41 reactions gives a new value in which the previous reactions are also present.
The Ignition Delay and Maximum temperature trend where it stabilizes is the step where we have the most efficient reduced mechanism i.e. That particular mechanism is safe to be used for that particular state values.
If you are interested more, check out my project here. If you have any questions, you can alsways reach out to me!
